 |
||||
| Навигация | |||||||||||||||
| Администрация | Студентам | Абитуриентам | Форум | Новости | Карта сайта | Создатели | |||||||||
|
2) Поле заряженного цилиндра: заряженный цилиндр радиуса R, (см. рис. 7), окружим
Согласно теореме Гаусса - Остроградского при где t = q/ h - линейная (погонная) плотность заряда, которая измеряется в Кл/м. Когда r < R, то 4) Поле заряженной сферы: поток вектора т.е. вне заряженной сферы поле такое же, как и поле точечного заряда той же величины, помещенного в центре сферы. Внутри сферы нет зарядов и поэтому поле там отсутствует, т. е. при г < R имеем |
||||
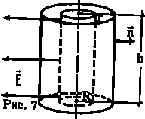
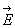 через основания равен нулю, т. к.
через основания равен нулю, т. к. 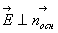 , где
, где 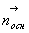 - внешняя нормаль к основаниям цилиндра; поток через боковую поверхность
- внешняя нормаль к основаниям цилиндра; поток через боковую поверхность 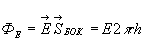 ,
,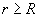
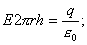
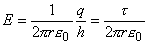 (9)
(9)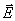 через поверхность сферы радиуса r,
через поверхность сферы радиуса r, 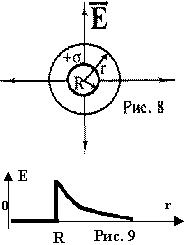 (см. рис. 8 ), которая окружает заряженную сферу, имеющую радиус R ,при r
(см. рис. 8 ), которая окружает заряженную сферу, имеющую радиус R ,при r 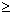 R
R 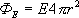 . По теореме Гаусса -Остроградского
. По теореме Гаусса -Остроградского 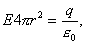 откуда
откуда 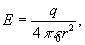 (10)
(10)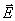 = 0. Это свойство используют для экранировки от полей внешних зарядов; график Е = f(r) для случая заряженной сферы приведен на рис. 9.
= 0. Это свойство используют для экранировки от полей внешних зарядов; график Е = f(r) для случая заряженной сферы приведен на рис. 9.