 |
||||
| Навигация | |||||||||||||||
| Администрация | Студентам | Абитуриентам | Форум | Новости | Карта сайта | Создатели | |||||||||
|
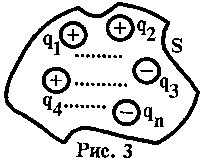
Согласно принципу суперпозиции
таким образом Итак, мы доказали теорему Гаусса - Остроградского: "ПОЛНЫЙ ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ЧЕРЕЗ ПРОИЗВОЛЬНУЮ ЗАМКНУТУЮ ПОВЕРХНОСТЬ РАВЕН АЛГЕБРАИЧЕСКОЙ СУММЕ ЗАРЯДОВ, ОХВАТЫВАЕМЫХ ЭТОЙ ПОВЕРХНОСТЬЮ, ДЕЛЕННОЙ НА Теорему Гаусса - Остроградского, (5), можно записать в дифференциальной форме:
Из теоремы Гаусса - Остроградского вытекают следствия: 1) линии вектора |
||||
 поэтому
поэтому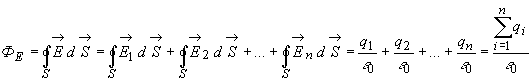 ,
, . (5)
. (5) "
" , (6)
, (6)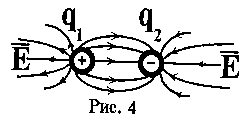
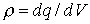 - объемная плотность заряда.
- объемная плотность заряда. , знак
, знак  - оператор набла.
- оператор набла.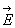 (силовые линии) нигде,кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4.); 2) если алгебраическая сумма зарядов, охватываемых замкнутой поверхностью, равна нулю, то полный поток через эту поверхность равен нулю; З) если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то число входящих линий вектора напряженности равно числу выходящих и поэтому полный поток через такую поверхность равен нулю.
(силовые линии) нигде,кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4.); 2) если алгебраическая сумма зарядов, охватываемых замкнутой поверхностью, равна нулю, то полный поток через эту поверхность равен нулю; З) если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то число входящих линий вектора напряженности равно числу выходящих и поэтому полный поток через такую поверхность равен нулю.