 |
||||
| Навигация | |||||||||||||||
| Администрация | Студентам | Абитуриентам | Форум | Новости | Карта сайта | Создатели | |||||||||
|
Установим изменение потенциальной и кинетической энергий колеблющейся системы. Известно, что потенциальная
энергия упруго деформированного тела равна
Кинетическая энергия
Анализ (7) и (8) показывает, что когда одна из энергий E=Wn+Wk=kA2/2 (9) остается величиной постоянной и для пружинного маятника, (см. рис. 1), она определяется работой, совершенной внешней силой по сжатию или растяжению пружины. Итак, мы рассмотрели свободные или собственные колебания, которые происходят в системе, предоставленной самой себе, после того, как она была выведена из положения равновесия. Но в реальных условиях всегда на механические системы действуют силы трения из-за чего свободные колебания переходят в затухающие, которые будут рассмотрены в параграфе 8. Векторная диаграмма гармонического колебания Гармоническое колебание
можно представить в виде проекции вектора Комплексная форма представления колебаний
Поэтому уравнение гармонического колебания (3) можно записать в экспоненциальной форме:
Вещественная часть Обычно обозначение
|
||||
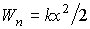 , где
k - коэффициент упругости, х - смещение; откуда для потенциальной энергии колебаний находим
, где
k - коэффициент упругости, х - смещение; откуда для потенциальной энергии колебаний находим
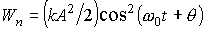 . (7)
. (7)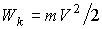 , что, согласно (2) и (5), в нашем
случае будет
, что, согласно (2) и (5), в нашем
случае будет
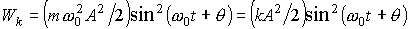 . (8)
. (8)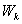 или
или
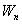 увеличивается, то другая уменьшается. Полная же энергия
увеличивается, то другая уменьшается. Полная же энергия
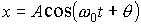
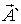 ,
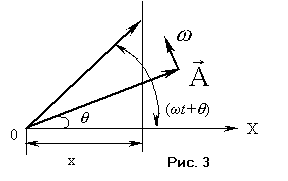
вращающегося против хода часовой стрелки с угловой скоростью, равной круговой частоте
,
вращающегося против хода часовой стрелки с угловой скоростью, равной круговой частоте
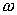 . Из рис. 3 следует, что проекция вектора
. Из рис. 3 следует, что проекция вектора
 на направление ОХ будет
на направление ОХ будет
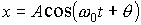 .
.
 Согласно формуле Эйлера для комплексных чисел
Согласно формуле Эйлера для комплексных чисел 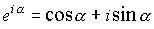 , где
, где
 .
.
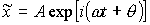 .
.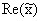 представляет собой смещение
х при гармоническом колебании
представляет собой смещение
х при гармоническом колебании 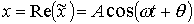 .
.
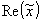 опускают и пишут так
опускают и пишут так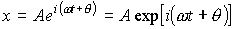 .
.